Camille Scalise

Math 300 Geometry

The following proof of Proposition 3.20, angle subtraction imitates the proof of Proposition 3.11 segment subtraction. Proposition 3.11 states, "If A*B*C, D*E*F, AB is congruent to DE, and AC congruent to DF, then BC is congruent to EF."

Proposition 3.20 states, "Given ray BG between BA and BC, EH between ED and EF, and angle <CBG is congruent to angle <FEH and angle <ABC is congruent to angle <DEF, then angle <GBA is congruent to angle <HED."

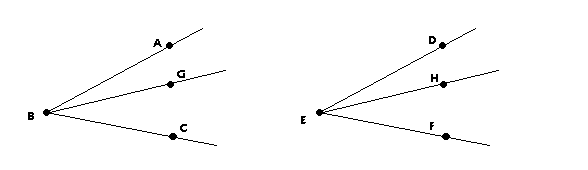
Although segments and angles are seemingly very different, there are several similarities which enable the proof of angle subtraction to be derived from the proof of segment subtraction. In segment subtraction, Proposition 3.11, we know that A, B, and C are distinct and collinear points by Betweeness Axiom 1. Point B lies between points A and C. Likewise in Proposition 3.20, there are three non-opposite rays emanating from a common point and it is given that ray BG is between BA and BC. These facts give us the important similarity of distinct objects and betweeness. In order to determine the proof of angle subtraction from the proof of segment subtraction, we wish to refer to angles in a manner similar to segments. For example, relabeling the three rays in Proposition 3.20 that form angle <ABC to HR, HS, and HT and the other rays of angle <DEF to JU, JV, and JW (See Figure 1). The segments in Proposition 3.11 can remain as given (See Figure 2).

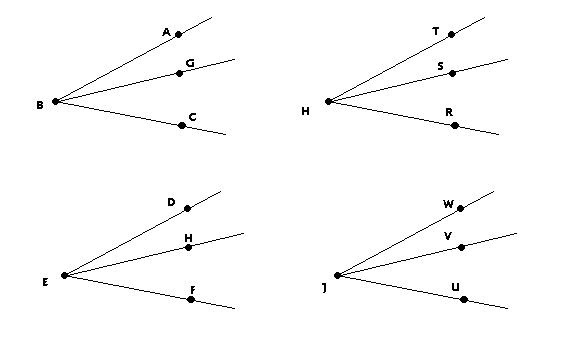
Figure 1. Relabeling angles of Propositions 3.20.

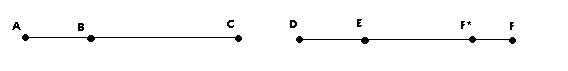
Figure 2. Labeling for Proposition 3.11.

In Proposition 3.11, B is between points A and C. Similarly, ray HS is in between rays HR and HT. Therefore, ray HS corresponds to point B. We can call this ray S to mimic the same terminology as a point on a segment. Also, there is angle <RHS which corresponds to segment AB. We can change this and give it notation similar to a segment by referring to this angle as RS. We can see each point on the segments in Proposition 3.11 corresponds to a ray in Proposition 3.20 and each segment corresponds to an angle. Now, we use the proof of segment subtraction to obtain the proof for angle subtraction by substituting the corresponding parts. The remaining corresponding parts are EF ~ VW, EF* ~ VW*, BC ~ ST, AB ~ SR, DE ~ UV, AC ~ RT, DF ~ UW, and DF* ~ UW*. The proof of Proposition 3.11 is as follows:

If A*B*C, D*E*F, AB congruent to DE, and AC congruent to DF, then BC is congruent to EF (See Figure 2).

1. There is a unique point F* on same side of E as F such that EF* is congruent to BC by Congruence Axiom 1.

2. It is given that segment AB is congruent to DE and by Betweeness Axiom 1 D, E, F, and F* are distinct.

3. By segment addition, AC is congruent to DF* but it is given that AC is congruent to DF so DF is congruent to DF* because of Congruence Axiom 2.

4. Since DF is congruent to DF* and F, F* are both on ray EF then F = F*.

5. Since F = F*, and EF* is congruent to BC, then EF is congruent to BC by Step 1, Step 3 and the Hypothesis.

Substituting the corresponding parts from our new notation, we now obtain the proof of Proposition 3.20. The justifications will also change but the outline of the proof remains the same.

Given ray S between T and R, V between W and U, angle <RS congruent to angle <UV and angle <RT congruent to angle <UW, then angle <ST is congruent to angle <VW.

1. There is a unique ray W* on the same side of V as W where same side means the ray is between angle <VW such that angle <VW* is congruent to <ST by Congruence Axiom 4 (see Figure 1).

2. It is given that angle <SR is congruent to <UV and by definition of angle and construction of W* all of the rays U, V, W, and W* are distinct.

3. By angle addition, <RT is congruent to <UW* but it is given that <RT is congruent to <UW and by Congruence Axiom 4 this angle is unique so <UW is congruent to <UW*.

4. Since <UW* is congruent to <UW and W and W* both form the same angle, then W = W*.

5. Since W = W* and <VW* is congruent to <ST then <VW is congruent to <ST by Step 1, Step 4 and the Hypothesis.

We have now determined a relationship between angle and segment subtraction. When beginning a proof, previous proofs may help outline the new proof. Being able to recognize relationships and similarities among different proofs can make new proofs easy to formulate.

References

Greenberg, Marvin J. Euclidean and Non-Euclidean Geometries. New York: W. H. Freeman and Company, 1993.